Connecting Local Knowledge to Global Behavior Using the Taylor Series

In my AP Calculus BC class, we recently explored Taylor series—a topic that combines mathematical precision with philosophical depth. As we worked through how derivatives at a single point can approximate a function's behavior nearby, I started thinking about how this process reflects larger ideas about knowledge and prediction. While Taylor series are tools for solving problems in calculus, they are also windows into how local information can illuminate broader patterns and behaviors.

What Is a Taylor Series?

The Taylor series uses information about a function's derivatives at a single point to approximate that function near the point. The formula for a Taylor series expansion around a point $a$ is:

$$f(x)\approx f(a)+f^{\mathrm{\prime }}(a)(x-a)+\frac{f^{\mathrm{\prime }\mathrm{\prime }}(a)}{2!}(x-a{)}^2+\frac{f^{(3)}(a)}{3!}(x-a{)}^3+\cdots$$

This formula is built step by step, incorporating more terms to reflect higher-order behaviors of the function. The zeroth term, $f(a)$, gives the function's value at the point. The first derivative, $f'(a)$, adds information about its rate of change. The second derivative, $f''(a)$, provides insight into the curvature, and so on. Each term adds more nuance to the approximation, bringing it closer to the true behavior of the function within a certain neighborhood around $a$.

But what really caught my attention is the philosophical idea buried in this formula: by studying a function at a single point, we can predict its behavior nearby. This idea feels weird, like finding a way to uncover global truths from local observations.

Local Knowledge and Approximation

The power of the Taylor series lies in its ability to turn information about derivatives at a single point into a meaningful approximation of the function in the vicinity. For example, the Taylor series for $\sin (x)\; around$$a = 0$ (the Maclaurin series) is:

$$\sin (x)\approx x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots$$

This series allows us to approximate $\sin(x)$ near zero with remarkable accuracy using only a few terms. The idea that we can approximate something as complex and periodic as $\sin(x)$ with just polynomials derived from a single point is both elegant and thought-provoking.

Visualization of the Taylor series approximations for y = sin(x) at x=0.

$<span\; style="text-align:\; center;">Each\; curve\; represents\; a\; higher-order\; polynomial\; approximation,\; showing\; how\; the\; series\; becomes\; more\; accurate\; near\; the\; point\; of\; expansion\; as\; more\; terms\; are\; added. </span>$("How to write Taylor's series of sinx in PSTricks?", Stack Exchange, https://tex.stackexchange.com/questions/512201/how-to-write-taylors-series-of-sinx-in-pstricks)

However, the limitations of this approach are just as striking. The Taylor series is most accurate near the point of expansion, but as we move further away, the errors grow unless the series converges perfectly. For some functions, like $\frac{1}{1+x^2}$, the series converges beautifully over a wide range. For others, such as $\ln(x)$ or $\arctan(x)$, the series diverges if $x$ moves too far from the point of expansion.

This raises a philosophical question: how far can we trust local knowledge to reveal broader truths? In calculus, as in life, approximations work best when the system behaves predictably, but the further we extrapolate, the more we risk encountering surprises.

The Power and Limits of Reductionism

Taylor series reflect a larger philosophical idea: reductionism. In reductionism, we try to understand complex systems by breaking them down into simpler, more manageable parts. For Taylor series, this means reducing a function’s behavior to its local properties (its derivatives at a point) and building from there. This approach works wonderfully for smooth, well-behaved functions, but it struggles when the function has discontinuities or sudden changes.

For example, consider the function:

$$f(x)=e^{-1\mathrm{/}{x}^2}\text{for }x\mathrm{\ne }0,f(0)=0.$$

This function is infinitely differentiable at $x = 0$, and all its derivatives at that point are zero. However, its Taylor series around $x = 0$ is simply $f(x) = 0$, which fails to represent the actual function anywhere except at the point itself. This discrepancy reminds us that while reductionism can provide valuable insights, it cannot capture every nuance of a system.

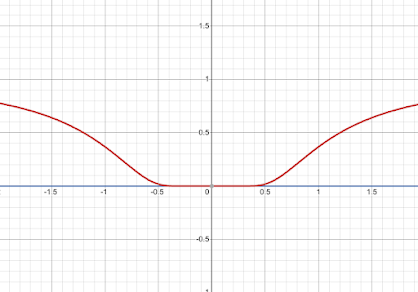The graph of $y = e^{-1/x^2}$ (red) compared to its Taylor series expansion $y = 0$ (blue) around $x=0.\mathrm{ }$ 

Despite being infinitely differentiable, the Taylor series fails to represent the function beyond the point of expansion, illustrating the limitations of reductionism in capturing global behavior from local data.

This same challenge appears in other fields. In science, we often analyze small, localized phenomena to build universal laws. For example, studying the behavior of particles in a controlled environment helps physicists develop models of matter and energy. But just like with Taylor series, there’s a limit to how far these models can be extrapolated before they lose accuracy.

Prediction and the Nature of Change

At the heart of the Taylor series lies the derivative, a mathematical tool that measures how a function evolves at a specific point. The Taylor series leverages these rates of change—its value, slope, curvature, and higher-order variations—to approximate the function’s behavior in a neighborhood around that point. Philosophically, this emphasizes an intriguing principle: understanding the dynamics of a system, rather than just its static properties, is key to making predictions about its behavior.

This focus on change aligns with a broader idea in many fields of study: systems are often best understood not by isolating their components but by examining how those components interact and evolve. In the Taylor series, the essence of a function is encoded in its derivatives—the ways it reacts to small changes—rather than in the function’s static value at a point. Similarly, in physics, understanding a particle’s motion requires knowledge of its velocity and acceleration, not just its position.

However, the Taylor series also demonstrates the limitations of prediction. It works well for functions that are smooth and continuous, where local behavior provides reliable clues about nearby points. But for functions with discontinuities or sharp transitions, the Taylor series quickly loses its predictive power. This limitation parallels challenges in real-world systems, where models based on local observations can fail to capture the complexity of broader patterns. In both cases, the tools we use to predict must be matched to the nature of the system itself.

The Taylor series, then, is more than just a mathematical approximation; it’s a reflection of how we approach understanding. It captures the dual nature of prediction: the ability to uncover patterns from localized data, balanced by an awareness of the boundaries within which those patterns hold true. Through this lens, the Taylor series serves as both a technical tool and a philosophical reminder of the interplay between knowledge and uncertainty.